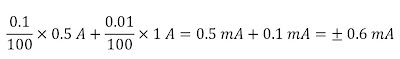So the accuracy of the power measurement (which is calculated from the individual voltage and current measurements) is dependent on the accuracy of the individual V and I measurements.
For example, you might use a multimeter to make V and I measurements and calculate power. The accuracy of these individual measurements is typically specified as a percent of the reading plus a percent of the range which is an offset. (Note that “accuracy” here really means “inaccuracy” since we are calculating the error associated with the measurement.)
Let’s use an example of measuring 20 Vdc and 0.5 Adc from which we calculate the power to be 10 W. We want to know the error associated with this 10 W measurement. Looking up the specs for a typical multimeter (for example, the popular Keysight 34401A), we find the following 1-year specifications:
DC voltage accuracy (100 V range): 0.0045 % of reading + 0.0006 % of range
DC current accuracy (1 A range): 0.1 % of reading + 0.01% of range
The error (±) associated with the voltage measurement (20 V) is:
So when the measurement reading is 20.0000 V, the actual voltage could be any value between 19.9985 V and 20.0015 V since there is a 1.5 mV error associated with this reading.
The error (±) associated with the current measurement (0.5 A) is:
So when the measurement reading is 0.5 A, the actual current could be any value between 0.4994 A and 0.5006 A since there is a 0.6 mA error associated with this reading.
We can now do a worst-case calculation of the error associated with the calculated power measurement which is the product of the voltage and current. The lowest possible power value is the product of the lowest V and I values: 19.9985 V x 0.4994 A = 9.98725 W. The highest possible power value is product of the highest V and I values: 20.0015 V x 0.5006 A = 10.01275 W. So the error (±) associated with the 10 W power measurement is ± 12.75 mW.
The above is the brute-force method to determine the worst-case values. It can be shown that the percent of reading part of the power measurement error can be very closely approximated by the sum of the percent of reading errors for the V and I. Likewise, it can be shown that the offset part of the power measurement error can be very closely approximated by the sum of the voltage reading times the current offset error and the current reading times the voltage offset error:
Applying this equation to the example above for the 100 V and 1 A ranges at 20 V, 0.5 A:
So for 10 W, we get:
As you can see, this is the same result as produced by the brute-force approach. Isn’t it great when math works out the way you expect?!?!
In summary, the error associated with a power measurement calculated as the product of a voltage and current measurement has two parts just like the V and I errors: a % of reading part and an offset part. The % of reading part is closely approximated by adding the % of reading parts for the V and I measurements. The offset part is closely approximated by adding two products together: the voltage reading times the current offset error and the current reading times the voltage offset error. It’s as simple as that!