Powerlifting Agilent style!

I have been working out at a gym including lifting weights since the early 1980’s. We have a small gym here in our office building that I use a few times per week. The other day, while doing incline bench presses, my mind was wandering and I began to wonder how much power it took for me to lift the barbell and weights.

I could put the barbell and weights on a battery operated lift we have here in the office and instead of the battery, use one of our power supplies to power the lift and measure the power while operating the lift. I also wanted to calculate how much power would be required. I admit that I had to take out my old physics book to refresh my memory on how to convert weight moved through a distance to watts, but this turned out to be pretty simple: the power is just the force (weight in newtons) times the velocity. Here is the justification:

Force is mass times acceleration. F = mass*acceleration = kg-m/s^2 = newton = N which is weight when the acceleration is due to gravity (weight = mass*gravity).

Work (energy) is force (weight) applied over distance. Work = F*distance = N-m = joule = J.

Power is work per unit of time. Power = J/s = watt = W.

So power in watts = W = J/s = N-m/s = kg-m/s^2-m/s = mass * acceleration * velocity = kg*gravity*velocity = weight*velocity (gravity = 9.8 m/s^2).

During my investigation, I did go off on a tangent for a short time looking at why we talk about measuring weight in kilograms even though kilograms are units for mass and not weight. It would be proper to measure weight in newtons, not in kilograms, but that’s a different story!

So when I lift 205 lbs (93 kg) a distance of 15 inches (0.38 m) in 1.5 seconds, I use 231 watts of power to do so (mass*gravity*velocity = 93 kg * 9.8 m/s^2 * 0.38 m/1.5 s). As I mentioned above, I wanted to see if I could measure something similar with a power supply connected to a battery operated lift by using our power supplies in place of the 24 V batteries. Here is what I found:

I did a baseline power measurement of just the lift lifting some wooden pallets needed to support the barbell I was about to put on the lift. I used 2 Agilent N7972A (40 V, 50 A, 2kW) power supplies connected in parallel (I needed the extra current capacity) and set to 24 V along with our 14585A Control and Analysis Software to capture the power over time. I could then add weight and measure the incremental power required to lift the added weight.

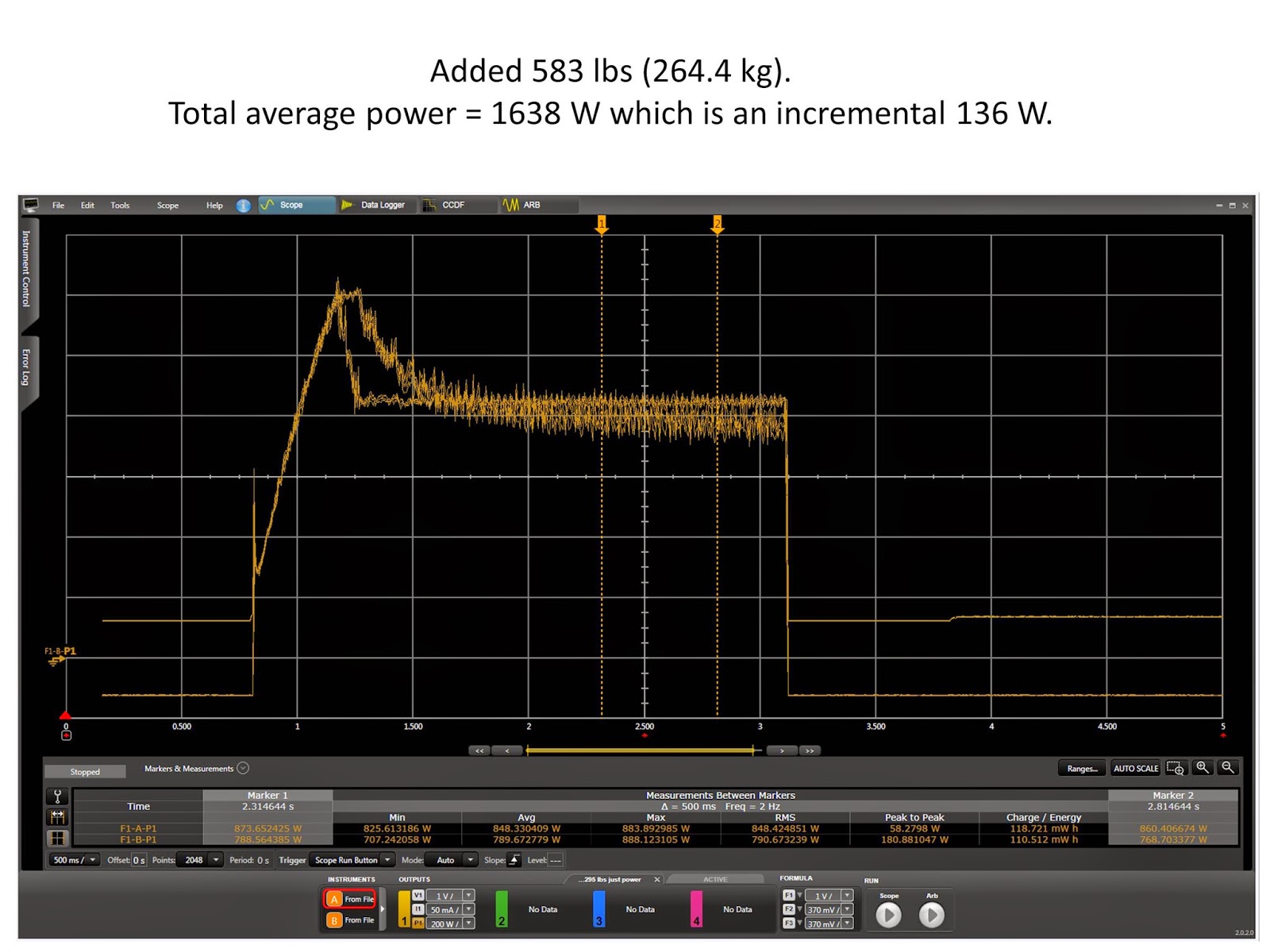
I found that the lift itself consumes 1502 W as my baseline measurement. Then I added a 288 lb (130.6 kg) battery compartment along with 295 lbs (133.8 kg) of barbell weighs for an added 583 lbs (264.4 kg). Again, I measured the power consumed by the lift while it moved the weights vertically and found it to be 1638 W. Lifting the incremental 264.4 kg consumed an additional 136 W. Let’s see if this makes sense with a calculation. The lift moved 4.5 inches vertically in 2.2 seconds which equals 0.052 m/s. The calculated power is then 264.4 kg * 9.8 m/s^2 * 0.052 m/s = 134.7 W. That’s very close to the measured 136 W!!

It is no surprise that the laws of physics work as expected here and that our power supplies can provide insight into those laws. Agilent has added new meaning to the term “powerlifting”!